
In Part 1 of this article I noted that a sine wave, perhaps created by a mass on a spring bouncing up and down, results in a single peak in the spectrum. If the spring gets more rigid as it gets compressed, the mass will move less in one direction than the other. We can describe the form of the wave this makes as distorted or clipped. When we pass this clipped wave through the FFT, we get harmonics or multiples of the fundamental frequency.
For example, if the mass bounced up and down 30 times per second, we would see a peak in the spectrum at 30 Hz. If it was clipped, we would also see peaks at 60, 90, 120 and 150 Hz etc. These are called harmonics.
Are Harmonics Real?
The question I posed is: Are the harmonics real? In other words, although the mass is still only bouncing up and down 30 times per second, is there actually real vibration occurring at 60, 90 and 120 Hz Etc? OR are these just artifacts of the FFT?
In Part 2 of the article I suggested an easy way to test the example I just presented. One could attach a spring or a tuning fork with a resonant frequency of 60 Hz to the spring system mentioned above. If there is no “real” 60 Hz vibration then the tuning fork will not make a sound.
In Part 2 of the article I also suggested that a single hit or impulse can be thought of the same way. If a tuning fork has a natural frequency of 60 Hz, it will not make a sound unless it is excited at 60 Hz. It does however make a sound when you strike it against your hip. This means that the single strike or single impulse must contain “real” vibration at 60 Hz. Although I did not hit the tuning fork 60 times per second, the single impulse “contains” that frequency. It is not just a by product of the FFT.

Non Linearity
Why are there frequencies in the output that do not exist in the input? If I bounce the mass on the spring up and down at 30 Hz, why do I also get frequencies at 60, 90, 120 Hz Etc? The answer is non-linearity. In a non linear system you get things in the output that were not present in the input. You can read more about that here: https://zencovibrations.com/linear-and-non-linear-vibrations/
An Example of Harmonics that are Real in a Different Way
There are a couple of interesting cases where harmonics are “real” in a different way. I’ll give you a hint: We like the sound of harmonics.
If you have a string connected at both ends, like a guitar string, the modes or natural frequencies are also harmonics. If for example the first mode or natural frequency is 30 Hz, the 2nd will be 60 Hz and the 3rd 90 Hz etc. The reason for this is that the modes break up the space into equal divisions create a pattern of “standing waves” whereby the vibration reinforces itself. If the wave shape doesn’t perfectly fit, the waves will be out of phase and will cancel out.
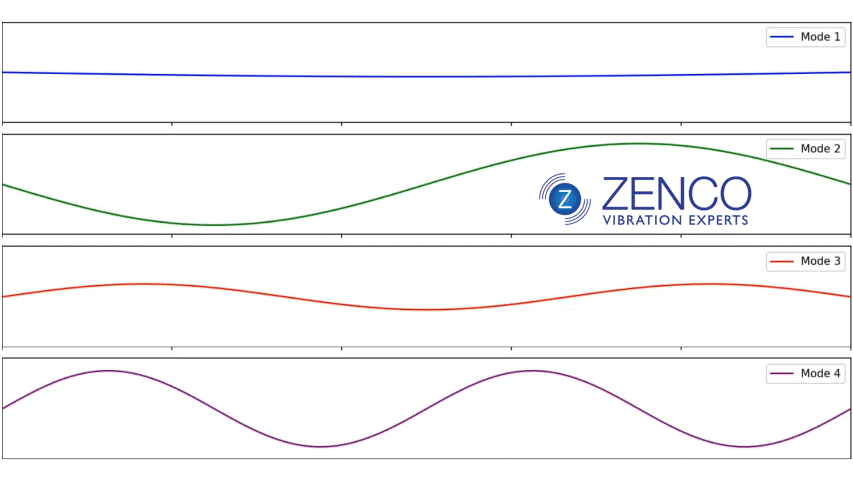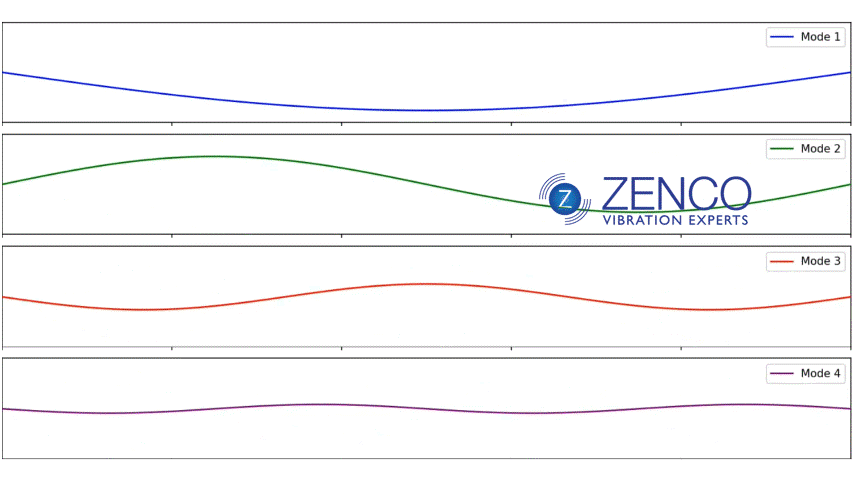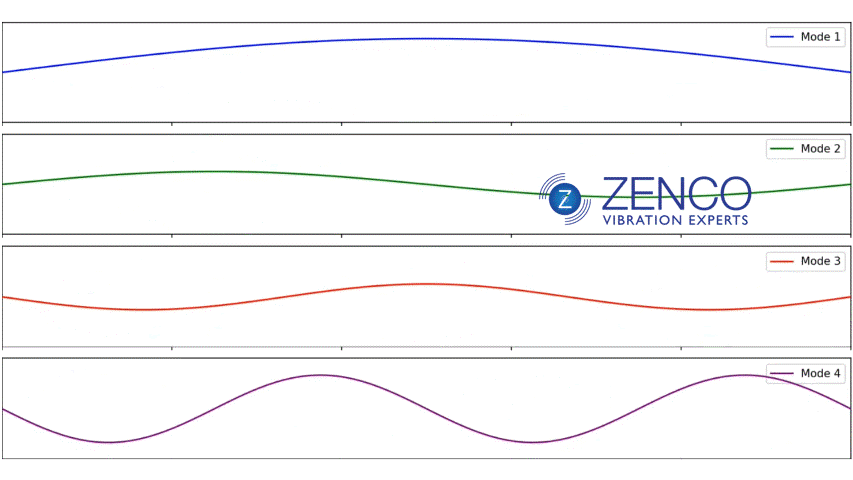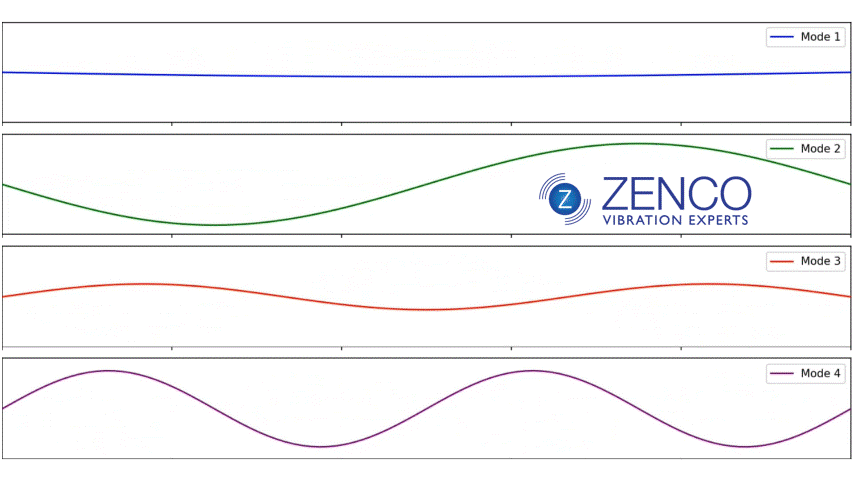
This is NOT true for most structures!!! In a bell, the first natural frequency might be 30 Hz, the 2nd might be 97.3 Hz and the 3rd might be 104.8 Hz. In other words, in most structures, the modes are NOT harmonics of each other.
Can you Think of Another Example?
Can you offer another example where the modes or natural frequencies are also harmonics? I gave you a hint that we like the sound of harmonics.
The other example is a tube filled with air – as in a pipe organ. In this case, the sound waves in the air bounce off then ends of the pipe. The wavelengths that perfectly fit in the space or that perfectly divide it up, will reinforce themselves. Those that don’t perfectly fit in the space will bounce back out of phase and will cancel each other out.
The fundamental frequency and harmonics generated by a pipe organ are therefore related to the length of the tube.
Keep your eyes open for another article in thus series where we’ll see what out AI overlords have to say about the reality of harmonics. In the meantime….
How About Registering for a Vibration Course?





